Полное сопротивление электрической цепи
Содержание
Понятие тока и напряжения
Закономерность учёного устанавливает зависимость между собой трёх электрических величин: тока, напряжения и сопротивления. Поэтому для того чтобы разобраться в сути закона Ома для полной электрической цепи, необходимо понимать, что же из себя они представляют.
 В любом теле существуют свободные элементарные частички, обладающие определённым количеством энергии — зарядом. Если тело находится в спокойном состоянии, то есть на него не оказывается никакого воздействия, то происходит их хаотичное перемещение. Если же к телу приложено электрическое поле, то их перемещение становится упорядоченным, и они начинают передвигаться в одну сторону.
В любом теле существуют свободные элементарные частички, обладающие определённым количеством энергии — зарядом. Если тело находится в спокойном состоянии, то есть на него не оказывается никакого воздействия, то происходит их хаотичное перемещение. Если же к телу приложено электрическое поле, то их перемещение становится упорядоченным, и они начинают передвигаться в одну сторону.
Такое направленное движение называют электрическим током. Мерой его служит сила тока, скалярная величина, определяемая отношением количества зарядов прошедших через поперечное сечение проводника за единицу времени: I = dq/dt. За единицу измерения силы тока принят ампер.
Если направление перемещения зарядов остаётся неизменным, то движение тока считается постоянным, а если изменяется — переменным. Возникновение тока возможно только в замкнутой цепи. Для того чтобы заряд переместился, приложенное поле должно выполнить работу. То есть затратить какую-то энергию для перемещения заряда с одной точки в другую. Если принять, что в начальном положении частичка обладает нулевым зарядом, то тогда переместившись, она уже будет иметь другое его значение. Разность между этими величинами называется разностью потенциалов или напряжением.
Для поддержания силы тока в полной цепи необходим источник, постоянно воздействующий на свободные заряды и поддерживающий разности потенциалов на различных участках цепи. Величина силы, которая действует на цепь, называется ЭДС. Физически она представляет собой отношение работы, затрачиваемой на передвижение заряда от одного своего полюса к другому, к значению заряда: E = A/q. Измеряется ЭДС, так же как и напряжение, в вольтах.
При перемещении заряд из-за особенностей строения кристаллической решётки вещества, он сталкивается с различными дефектами и примесями. В результате этого происходит частичное рассеивание его потенциала, а скорость движения замедляется. Потеря энергии характеризуется электрической величиной-сопротивлением. Другими словами, сопротивление — это величина, препятствующая прохождению тока.
Вычисление импеданса
Идеальные элементы
Для резистора импеданс всегда равен его сопротивлению R и не зависит от частоты:
| zR=R{\displaystyle z_{R}=R} | (2) |
Конденсатор
Ток и напряжение для конденсатора связаны соотношением:
| i(t)=CdUdt.{\displaystyle i(t)=C{\frac {dU}{dt}}.} | (3) |
Отсюда следует, что при напряжении
| u^(jω,t)=U(ω)ej(ωt+ϕu(ω)){\displaystyle {\hat {u}}(j\omega ,t)=U(\omega )e^{j(\omega t+\phi _{u}(\omega ))}} | (4) |
ток, текущий через конденсатор, будет равен:
| i^(jω,t)=Cddt(U(ω)ej(ωt+ϕu(ω)))=jωCU(ω)ej(ωt+ϕu(ω)).{\displaystyle {\hat {i}}(j\omega ,t)=C{\frac {d}{dt}}\left(U(\omega )e^{j(\omega t+\phi _{u}(\omega ))}\right)=j\omega CU(\omega )e^{j(\omega t+\phi _{u}(\omega ))}.} | (5) |
После подстановки (4) и (5) в (1) получаем:
| z^C(jω)=1jωC=−jωC.{\displaystyle {\hat {z}}_{C}(j\omega )={\frac {1}{j\omega C}}=-{\frac {j}{\omega C}}.} | (6) |
Катушка индуктивности
Аналогичное рассмотрение для катушки индуктивности приводит к результату:
| z^L(jω)=jωL.{\displaystyle {\hat {z}}_{L}(j\omega )\;=j\omega L.} | (7) |
Общий случай
Для произвольного двухполюсника, состоящего из элементов с известным импедансом, нет необходимости производить приведенные выше вычисления с целью нахождения импеданса. Импеданс находится по обычным правилам расчёта сопротивления сложной цепи, то есть используются формулы для сопротивления при параллельном и последовательном соединении резисторов. При этом все математические операции производятся по правилам действий над комплексными числами. Например, импеданс идеальных последовательно соединенных резистора, конденсатора и катушки индуктивности будет равен:
| Z^(jω) =R+1jωC+jωL=R−jωC+jωL=R+j(−1ωC+ωL).{\displaystyle {\hat {Z}}(j\omega )\ =R+{\frac {1}{j\omega C}}+j\omega L=R-{\frac {j}{\omega C}}+j\omega L=R+j\left(-{\frac {1}{\omega C}}+\omega L\right).} | (8) |
Параллельное и последовательное соединение элементов
В разделе электротехники присутствует несколько вариантов того, как подключить детали в электрическую цепь. Есть параллельное и попеременное подсоединения. Их объединяет смешанная схема, которая представлена ниже.
Последовательное подключение — это когда все источники соединяются друг с другом последовательно. Получаемая цепь не обладает никакими разветвлениями. Сила тока в данном случае проходит через каждый источник. Она постоянная, общее напряжение одинаковое.
В случае препятствия резисторов заряду при последовательном подключении получится, что сопротивляемость будет равна сумме всех взаимозаменяемых пассивных элементов цепи. Рассчитывая параметры электротехнической схемы, не нужно применять частные параметры устройств. Их можно заменить одним значением, которое равно их суммарному показателю.
Обратите внимание! Польза взаимозаменяемости компонентов заключается в возможности замены нескольких пассивных элементов электрической сети одним. Соединение элементов
 Соединение элементов
Соединение элементов
Параллельное подключение — это такое подсоединение источников, в котором входы всех устройств находятся в одних местах, а выходы — в других. Этими местами служат узлы.
В случае эквивалентного препятствия заряду при параллельном соединении определить его можно благодаря закону Ома с преобразованием формулировки подсчета. Так, сделать необходимый расчет можно, основываясь на следующей формуле: R · R / N·R = R / N.
Если это соединение нескольких индуктивных катушек, то их индуктивный показатель сопротивляемости будет рассчитываться по той же формуле, что для резисторных устройств.
Важно! В случае с параллельным подключением общий показатель будет меньше любого показателя резистора. При последовательном подсоединении все наоборот
Аналогия с электрическим сопротивлением проводника на примере резистора
Резистор — пассивный элемент, обладающий чисто активным сопротивлением. Реактивная составляющая комплексного сопротивления резистора равна нулю, так как соотношение между напряжением на резисторе и током через него не зависит от частоты тока/напряжения, а так же из-за того, что резистор является пассивным элементом (поскольку не содержит внутренних источников энергии). Если к его концам приложить некоторое напряжение U (подсоединить источник напряжения), то через резистор пойдёт электрический ток I. Если через резистор пропустить электрический ток I (подсоединить источник тока), то между концами резистора возникнет падение напряжения U. Резистор характеризуется электрическим сопротивлением, которое равно отношению напряжения U, к току I (см. закон Ома для участка цепи):
- R=UI.{\displaystyle R={\frac {U}{I}}.}
Применение понятия «электрическое сопротивление» к реактивным элементам (катушка индуктивности и конденсатор) при постоянном токе приводит к тому, что:
сопротивление идеальной катушки индуктивности стремится к нулю:
- если пропустить через идеальную катушку индуктивности некоторый постоянный ток I, то при любом значении I, падение напряжения на катушке будет нулевым:
- U=;{\displaystyle U=0;}
- R=UI=I=;{\displaystyle R={\frac {U}{I}}={\frac {0}{I}}=0;}
сопротивление идеального конденсатора стремится к бесконечности:
- если приложить к конденсатору некоторое постоянное напряжение U, то при любом значении U, ток через конденсатор будет нулевым:
- I=;{\displaystyle I=0;}
- R=UI=U=∞.{\displaystyle R={\frac {U}{I}}={\frac {U}{0}}=\infty .}
Это справедливо лишь для постоянного тока и напряжения. В случае же приложения к реактивному элементу переменного тока и напряжения, свойства реактивных элементов существенно иные:
- напряжение между выводами катушки индуктивности не равно нулю;
- ток, протекающий через конденсатор, не будет равен нулю.
Такое поведение не может быть описано в терминах активного сопротивления для постоянного тока, поскольку активное сопротивление предполагает постоянное, не зависящее от времени соотношение тока и напряжения, то есть отсутствие фазовых сдвигов между током и напряжением.
Было бы удобно иметь некоторый параметр аналогичный активному сопротивлению и для реактивных элементов, который бы связывал ток и напряжение на них подобно активному сопротивлению в формуле закона Ома для постоянного тока.
Такую характеристику можно ввести, если рассмотреть свойства реактивных элементов при воздействиях на них гармонических сигналов. В этом случае ток и напряжение оказываются связаны некой константой (подобной в некотором смысле активному сопротивлению), которая и получила название «электрический импеданс» (или просто «импеданс»). При рассмотрении импеданса используется комплексное представление гармонических сигналов, поскольку именно в таком представлении одновременно учитывается и амплитудные, и фазовые характеристики гармонических сигналов и откликов систем на гармоническое воздействие.
Обобщенный импеданс в s-плоскости и преобразование Лапласа
Импедансы, определённые через комплексную частоту jω{\displaystyle j\omega }, позволяют вычислять частотный отклик некоторой линейной цепи, возбуждаемой гармоническим сигналом, причём только в установившемся режиме. Для расчёта отклика цепи на сигнал, произвольно изменяющийся во времени применяется обобщенный импеданс — функции комплексной переменной s=σ+jω{\displaystyle s=\sigma +j\omega } и отклик цепи во временно́й области вычисляется через обратное преобразование Лапласа, причем в таких вычислениях возбуждающий сигнал fin(t){\displaystyle f_{in}(t)} из временного представления должен быть предварительно преобразован в комплексное представление Ft(s){\displaystyle F_{t}(s)} через прямое преобразование Лапласа:
- Ft(s)=∫∞fin(t)e−stdt.{\displaystyle F_{t}(s)=\int _{0}^{\infty }f_{in}(t)e^{-st}\,dt.}
Комплексный отклик системы выражается обычным способом через преобразованное комплексное представление возбуждающего сигнала и комплексную передаточную функцию системы H(s){\displaystyle H(s)}:
- Ft,H(s)=H(s) Ft(s).{\displaystyle F_{t,H}(s)=H(s)\ F_{t}(s).}
| Двухполюсник | Обобщённыйимпеданс |
|---|---|
| Резистор | R{\displaystyle R\,} |
| Катушкаиндуктивности | sL{\displaystyle sL\,} |
| Конденсатор | 1sC{\displaystyle {\frac {1}{sC}}\,} |
Комплексная передаточная функция вычисляется обычным методом расчёта электрических цепей, например, по правилам Кирхгофа, в формулы в качестве сопротивлений подставляются обобщённые импедансы. Обобщённые импедансы пассивных двухполюсников приведены в таблице. Например, обобщённый импеданс цепи, состоящей из последовательно включённых резистора и катушки индуктивности будет R+sL{\displaystyle R+sL}.
Отклик цепи во временно́й области вычисляется обратным преобразованием Лапласа:
- fF,H(t)=L−1H(s) Ft(s)=12πi∫σ1−j⋅∞σ1+j⋅∞estH(s) Ft(s)ds,{\displaystyle f_{F,H}(t)={\mathcal {L}}^{-1}={\frac {1}{2\pi i}}\int \limits _{\sigma _{1}-j\cdot \infty }^{\sigma _{1}+j\cdot \infty }e^{st}H(s)\ F_{t}(s)\,ds,}
- где σ1 {\displaystyle \sigma _{1}\ } — некоторое вещественное число, выбираемое из условий сходимости интеграла.
- Пример вычисления временно́го отклика RC-фильтра нижних частот на ступенчатое возмущение
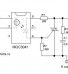
Пассивный RС-фильтр нижних частот 1-го порядка
Простейший фильтр нижних частот 1-го порядка изображён на рисунке и состоит из последовательно соединённых резистора и конденсатора, образующего делитель напряжения для входного сигнала где выходной сигнал снимается с конденсатора, обобщённый комплексный коэффициент передачи HRC(s){\displaystyle H_{RC}(s)} такого делителя:
- HRC(s)=1sCR+1sC=1sRC+1=1sT+1,{\displaystyle H_{RC}(s)={\frac {1/sC}{R+1/sC}}={\frac {1}{sRC+1}}={\frac {1}{sT+1}},}
- где обозначено T=RC{\displaystyle T=RC} — постоянная времени RС-цепи.
Ступенчатый входной сигнал можно выразить через функцию Хевисайда h(t){\displaystyle h(t)}:
- Uin(t)=U h(t),{\displaystyle U_{in}(t)=U_{0}\ h(t),}
- где U{\displaystyle U_{0}} — амплитуда ступеньки.
Преобразование Лапласа входного сигнала:
Fin(s)=LU h(t)=∫∞e−stUh(t)dt=Us.{\displaystyle F_{in}(s)={\mathcal {L}}=\int \limits _{0}^{\infty }e^{-st}\,U_{0}\,h(t)\,dt=U_{0}/s.}
- Uout(t)=L−1HRC(s) Fin(s)=12πi∫σ1−j⋅∞σ1+j⋅∞est1sT+1⋅Usds=U(1−e−tT).{\displaystyle U_{out}(t)={\mathcal {L}}^{-1}={\frac {1}{2\pi i}}\int \limits _{\sigma _{1}-j\cdot \infty }^{\sigma _{1}+j\cdot \infty }e^{st}{\frac {1}{sT+1}}\cdot {\frac {U_{0}}{s}}\,ds=U_{0}(1-e^{-t/T}).}
Таким образом, получен отклик цепи при нулевом начальном условии (UC={\displaystyle U_{C}=0} при t={\displaystyle t=0}), такой же, как и при применении другого метода расчёта, например, из решения обыкновенного дифференциального уравнения.
Для практического применения расчета цепей (и других расчётов) составлены подробные таблицы прямого и обратного преобразования Лапласа многих часто встречающихся при расчётах функций.
Комбинируя преобразование Лапласа с использованием его свойств и интеграл Дюамеля обычно относительно легко найти отклики во временной области самых различных линейных электрических цепей.